Intrackability: Characterizing Video Statistics and Pursuing Video Representations

Haifeng Gong and Song-Chun Zhu

This is a video clip taken at a memorial site at Malibu in 2009. Each flag represents a victim in the 9-11 event. For flags in the front, one can track the elements in motion, whileas for flags far away, one loses track of the elements and perceives a textured motion phenomenon. In between, there is a transition of our catastrophic transition in human perception and underlying representations (models) triggered by information scaling (camera zoom, object density and occlusion, motion dynamics). Studying this problem is key to understanding motion perception and developing realistic motion models for tracking and recognition.

Introduction

This work presents an information theorestical study of representatios for video tracking and their inferential uncertainly. In nature scenes, a wide variety of motion patterns are observed. These videos have different complexity and create different perceptual effects. In the literature of video modelling, there are mainly three classes of representations for trackable motions, i.e. motion vetors of contours, motion vectors of kernels, and motion vectors of points, sparse, or dense. For intrackable motion, inter-frame joint appearance representations are the most popular. When scale changes, representations need to change accordingly, as shown in Fig. 1. Inferential uncertainty of tracking is essential for representation selection. Intrackabilities can be used to select features for tracking.

We will give an insightful analysis of video intrackability and make the following contributions

1. We define intrackability quantitatively to measure the inferential uncertainty of representation on given video ensemble.
2. We characterize video regimes by intrackabilities.
3. Intrackability is used to select the most robust feature for tracking.
4. Based on our intrackability measure, some theoretical studies are given to justify empirical observations and intuitions, e.g. how the factors such as video resolution, and object dynamics affect the inferential uncertainty.
5. We show an idea for switching representation online for video tracking, guided by intrackability.
Fig. 1 Representation switches triggered by scale: (a) at high resolutions, we can describe the contour of an object; (b) at middle resolution, we can use a bounding box to represent an object; (c) at low resolution, we can use feature point to represent an object.

Statistical Characteristics of Video Complexity

There is a continuous transition between trackable motion and intrackable motion. In Fig. 2, 202 bird videos are embedded in the two dimensions spanned by the two eigen-vectors. Two major changes between the most intrackable (flat video on the upper-left corner) and the most trackable (large grained texture on the upper-right corner) are represented by two curves.

The simplest videos are blank ones composed of images with a uniform color. They can be treated as structural video, because each frame of them is a large flat region. They can also be treated as textured video with the smallest texture granularity. On the other extremeness, if videos are populous and contain many similar objects at similar small scale and nearly uniformed distributed positions, and each single object is still discernible, thus they can be treated as structural, and they can also be treated as textured because there are many repetitive patterns, though of large granularities.

Fig. 3 shows two typical transitions between two extrmities: blank video and extremely crowded one. The first is to add objects into a blank video gradually and the second is to increase the granularity of a populous video.

Fig. 4 shows the process of scale changing. If we keep the number of object to be one or very small, and zoom the video, another loop can be obtained.

The video regimes can be characterized by their tracking uncertainties, or intrackabilities.
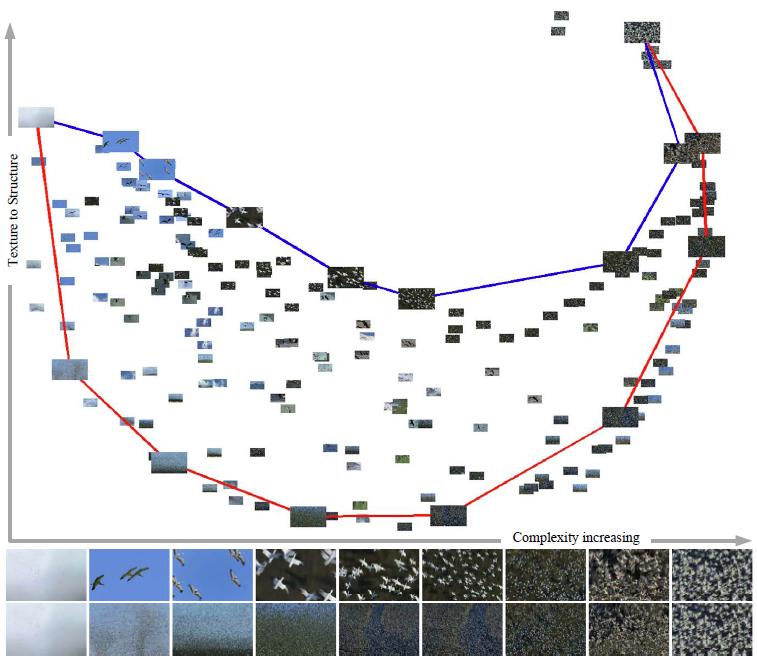Fig. 2 PCA embedding of histograms of intrackabilities of bird videos, two dimensions are composed of one through hundreds of thousands of birds at a wide range of scales. Red and blue curves show two typical transitions in natural videos. The blue curve shows videos form fewer structural elements (of objects) to more of them. The red curve shows videos from textured elements with smaller granularity to larger granularity. In the bottom, the first line shows video examples of the first transition (blue curve) and the second line shows the second transition (red curve).
Fig. 3 Illustrations of video regimes and typical transitions across them.
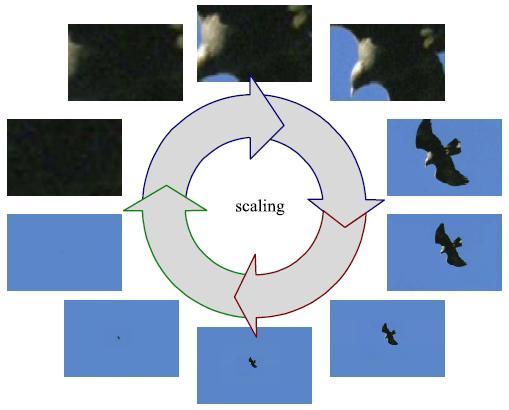Fig. 4 Effectis of videos of single object at a wide range of scales.

Intrackability and Representation

    Intracability on a single video is defined as the entropy of conditional probability and the value can be exactly computed, or approximated. While an algorithm searching for the optimal solution in a solution space, the score on the route can be converted to probabilistic scores, then an entropy can be estimated from these probabilistic scores.

    Different classes of representations are at different levels of details and different levels of computing burdens. Therefore, we propose a way to create hybrid representation composed of more than one typical representations automatically. The algorithm is divided into two steps. First, representation projections are applied to obtain trackable and orientedly trackable areas (see Fig. 5 ). Second, combing operations are applied in those areas to obtain a hybrid representation.
    Detailed Steps:
    1) Compute frame-pair intrackability map and oriented intrackability map;
    2) Apply threshold on intrackability map and oriented intrackability map to obtain trackable and orientedly trackable areas. Find the best threshold that achieves the lowest score.
    3) Pursue representations in different areas.

    Results of test on videos are shown in Fig. 6.

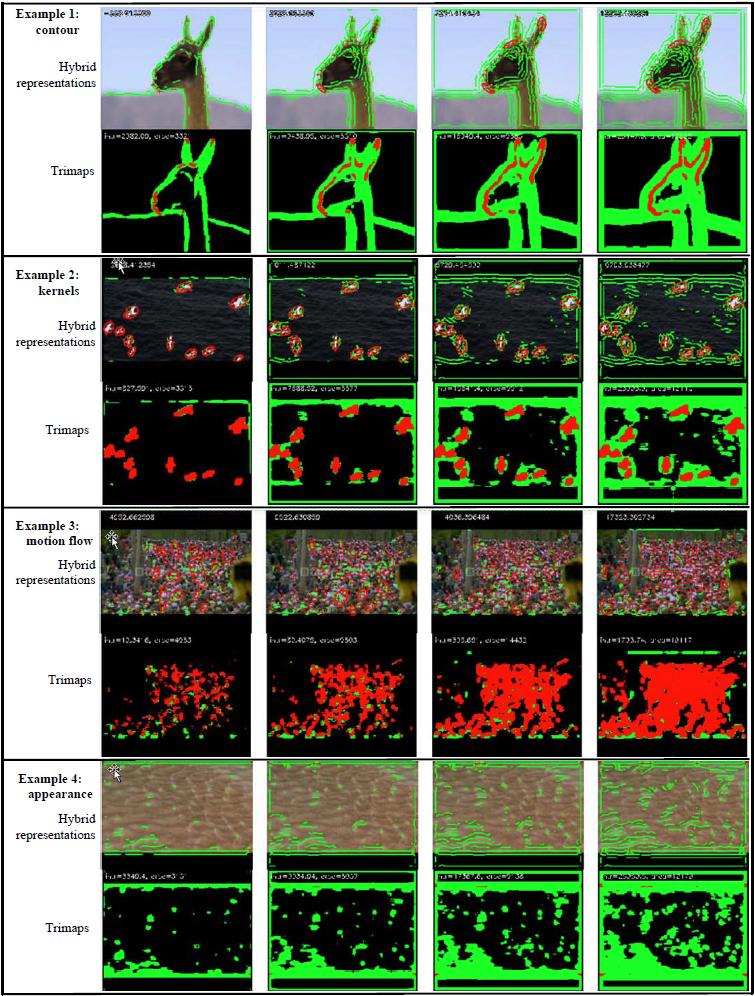Fig. 5 Trimaps and hybrid representations at different thresholds: reg-tracable points, green-oriented-trackable points, black-intrackable points. From left to right, threshold varies from hight to low. The first video can be best represented by contours. The second video can be best represented by kernels. The third viedo can be best represented by dense points. The forth can be best represented by appearance models.
Fig. 6 Results of hybrid representation pursuit, in each block: left-representations, green curves are trackable contours, crosses are trackable points and ellipses are grouped dernels; right-score curves, red is the intrackability, black is the total score. Asters on the black curves indicate the minima.

Intrackability in Tracking

    Point Tracking: We introduce intrackability pursuit to separated trackable points from a pair of images based on SSD tracking. For each point in the image, a small patch around it is used as its feature descriptor. And when computing intrackability for each point, we select them one by one. After one point is selected, its correlated neighbors are inhibited.

    Detailed Steps:

    1) For each patch, compute the intrackability and apply threshold to obtain the trackable areas.
    2) Select the most trackable patches in the trackable areas by intrackability pursuit.
    3) Output all selected patches.

    Line Tracking: We first project the motion vectors to all possible quantized orientations to compute the inatrackability of the projected components, and record the intrackability of the most trackable components in a projected intrackability map, and the corresponding orientation in an orientation map. Then a threshold is applied to obtain projected trackable areas. In these areas, we enumerate all possible combined lines and compute the corresponding intrackabilities. Finally, we select trackable lines one by one using their intrackability as indicators, and after one line is selected, the overlapping ones are inhibited.

    Detailed Steps:

    1) For each patch, for all quantized orientations, compute intracability. Find the most trackable orientation for each patch, record the minimum as oriented
    intrackability. Apply threshold to obtain the oriented trackable areas.
    2) Enumerate all possible lines with quantized orientations and lengths, in the oriented trackable area. The lines are consist of side-by-side patches with similar orientation.
    3) Let all patches on each line share the same motion. Computer the combined intrackability of these lines.
    4) Select the most trackable lines by pursuit.
    5) Output all selected lines.

    Three videos are tested and the results are shown in Fig. 7 .

Fig. 7 Results of video representation pursuit. (a) shows the intrackability map, darkness means low intrackability value. (b) shows the selected points, and (c) shows the selected lines. The number of points and lines are chosen more than necessary for demonstration purpose. Algorithms need only several top ones due to computation burden.

Related Publication:

Haifeng Gong and Song-chun Zhu, Intrackability: Characterizing Video Statistics and Pursuing Video Representations, IJCV [under revision] [pdf].