Introduction

Aerial image understanding is an important field of research for tackling the problems of automated navigation, large scale 3D scene construction, and object tracking for use in event detection. Most of the tasks using aerial images need or would benefit from a full explanation of the scene, consisting of the locations and scales of detected objects and their relationships to one another. Being able to identify objects of many different types and understand their relationships to one another gives a deeper understanding of the data and allows subsequent algorithms to make smarter decisions faster.

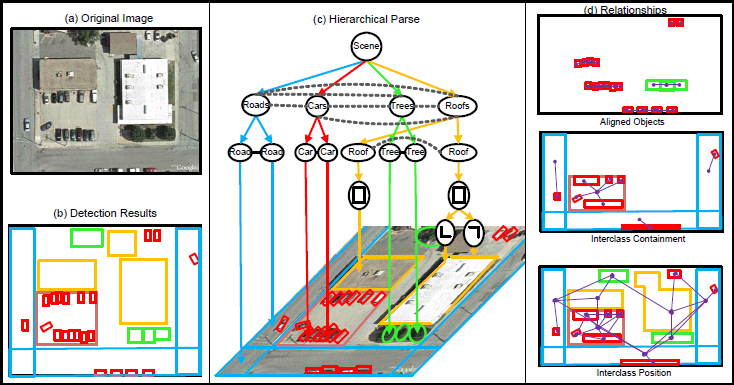
figure 1: An example of a hierarchically parsed aerial image. (a) The original image. (b) A flat configuration of objects in the scene. (c) A hierarchical parse graph of the scene. (d) Three typical contextual relationships and the objects related by them.

There are difficulties in aerial image parsing that do not arise in more restricted recognition tasks. Three major obstacles to modeling aerial images are:

We present a 3-layer hierarchy with embedded contextual constraints along with a 3-stage inference algorithm to solve the problems above and capture the natural hierarchical and contextual nature of aerial images.

Hierarchical and Contextual Model

To handle the large structural variations of aerial images we model scenes as groups of like objects, such as cars aligned in rows or roofs clustered into city blocks (see Figure 1). This abstracts the scene into loosely related neighborhoods. We then add statistical constraints within and between these groups to constrain their relative appearances, such as how close together they are or what size they are. We achieve this by embedding Markov random fields (MRFs) into a hierarchical grammar model. Our grammar model begins at a root scene node that then probabilistically decomposes into a number of group nodes, such as n groups of cars or m groups of roofs. Each of these groups can in turn decompose into a number of single nodes, such as j cars in one group, k cars in another. Alone this hierarchy only captures the frequency of objects, however, so we add contextual relationships via MRFs on the neighborhoods within each group and between groups. In this way we create a statistical model that uses a small set of decomposition rules to generate variable number of objects whose appearances are constrained by statistical relationships.

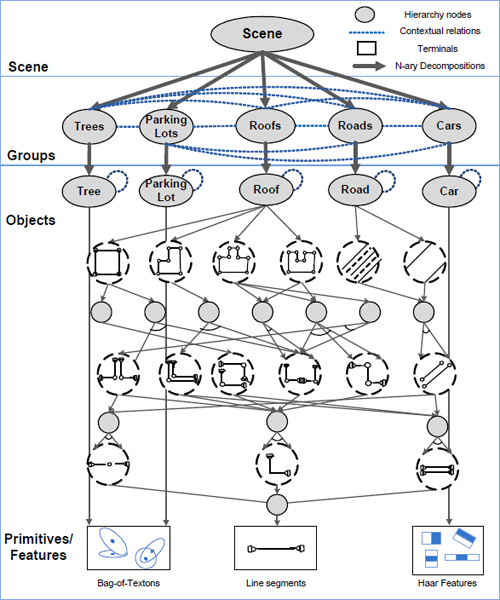
figure 2: The 3-level contextual hierarchy. The scene is broken down into groups of objects of one of five categories, which are in turn broken down into individual objects of the same type. The thick vertical arrows between the scene and groups and between the groups and objects indicate that these nodes can decompose into a variable number of children. Objects are represented by detectors, some of which (roofs, roads) are hierarchical themselves. The horizontal lines between nodes at the same level represent statistical constraints on the nodes’ appearance.

Automatic Learning of Context by Relationship Selection

Creating the constraints for our model by hand is infeasible due to the huge number of potential constraints that could exist, so we present an algorithm to automatically add statistical constraints to the hierarchy in a minimax entropy framework. This minimax entropy technique was used previously in texture modeling (Zhu et al) and on more general graphical models but we are now applying it to a hierarchical model. We seek to model the true distribution of aerial images, f, with our learned distribution, p, by iteratively matching feature statistics between f and p. This matching entails extracting features from a set of observed data (which follows f) and adjusting our model p such that it reproduces the statistics of these features. This learning method automatically selects the most important feature statistics to match and ignores low-information features. This allows us to add only relevant relationships from a large dictionary of potential constraints. By the end of this process, samples from p appear similar to true samples from f along the learned dimensions.

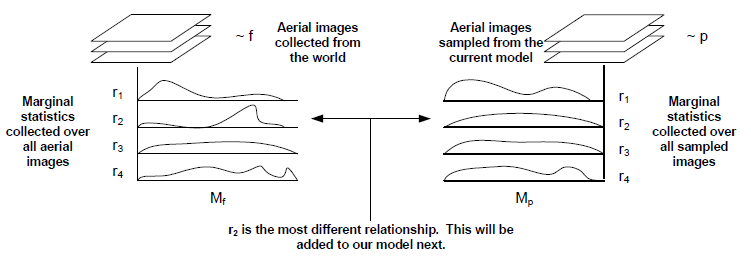
figure 3: A visualization of the learning process. Feature statistics Mf and Mp are computed over a set of aerial images and a set of aerial images sampled from our current model p, respectively. The most different of these, in this case r2, is selected to be added to our model. During the next iteration r2 will now match between Mf and Mp for newly sampled images from p. This process continues until no feature statistics differ significantly between the two sets of images.

Top-Down Bayesian Inference with Cluster Sampling and Prediction

To handle the coupling constraints that appear in aerial images we use a sampling algorithm inspired by Swendsen-Wang clustering. Swendsen-Wang cluster sampling was introduced to sample the Potts model more effectively by updating a cluster of sites at once instead of just a single site. Our variant of this algorithm, named Clustering via Cooperative and Competitive Constraints (C4) (Porway et al), updates multiple clusters at once, allowing us to move very rapidly in the solution space. The clusters represent competing explanations of the scene. For example, a patch explained by a parking lot with cars may be better explained by a single roof. To swap these explanations, we couple the cars with the parking lot and switch the whole cluster with the roof in a single step. This process results in an explanation of the scene with very few false positives. We also use the hierarchical nature of our top-down model to propose new objects our object detectors may have missed, thus increasing the number of true positives in our final result.

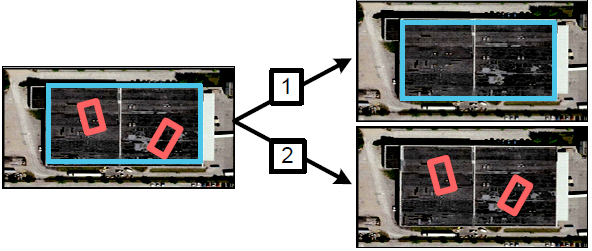
figure 4: An example of two choices a greedy inference algorithm could make for interpretations of the scene. Because cars cannot appear on top of roofs (let us assume the data supports this) selecting the roof in decision 1 eliminates the car nodes while selecting the cars in decision 2 does the opposite. The algorithm is stuck with this decision no matter what later evidence it may find.

The C4 algorithm allows inference to be computed on graphical models with both cooperative and competitive constraints. Much like how the Swendsen-Wang algorithm operates on an Ising model, C4 draws samples in two steps. In the first step edges are turned off independently and probabilistically according to the strength of the constraints. In the second step, a cluster of proposals connected by the remaining edges is uniformly selected and their on/off states are flipped. Figure 5 illustrates the basic operation of the algorithm.

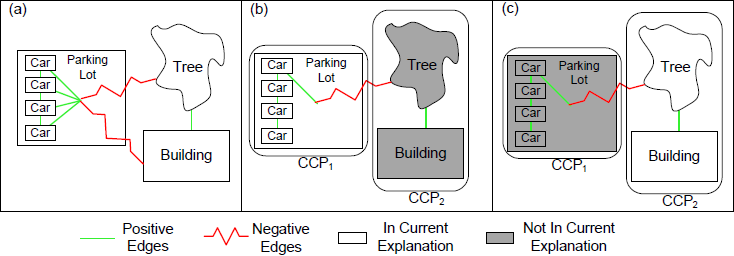
figure 5: An application of C4 to a toy aerial image. (a) Compatible object proposals (cars in the parking lot, the tree next to the building) are connected by positive edges while non-compatible proposals (tree with parking lot, building with parking lot) are connected by negative edges. (b), (c) C4 groups objects based on these connections and updates the state of the system to swap between alternate explanations.

Different bottom-up detectors are used for each type of object. Cars are trained with a discriminative AdaBoost classifier. Parking lots and trees are classified using TextonBoost, which combines color and shape cues in a boosting framework. Roofs and roads are detected using Compositional Boosting (T.F Wu et al), which combines low level line and corner junctions into higher level structures. Examples of the bottom-up detection results are shown in figure 6.

figure 6: Single object detections using our bottom-up detectors.

In the top-down phase of the algorithm, the generative nature of the model can be exploited to predict the location of missing objects. Figure 7 illustrates a random sample drawn from the model and validates that our model captures typcial scenes observed from the training data.

figure 7: A sample drawn from our learned model (blue = roofs, red = cars, black = roads, green = trees). These are not images directly sampled from the training data, but collections of objects obeying the statistics of our learned model. We can create a vast amount of unique object configurations even though we’ve never observed them directly.

Results

Figure 8 shows flattened configurations of the highest probability parse graph for each scene. We can see that the majority of objects are detected accurately.

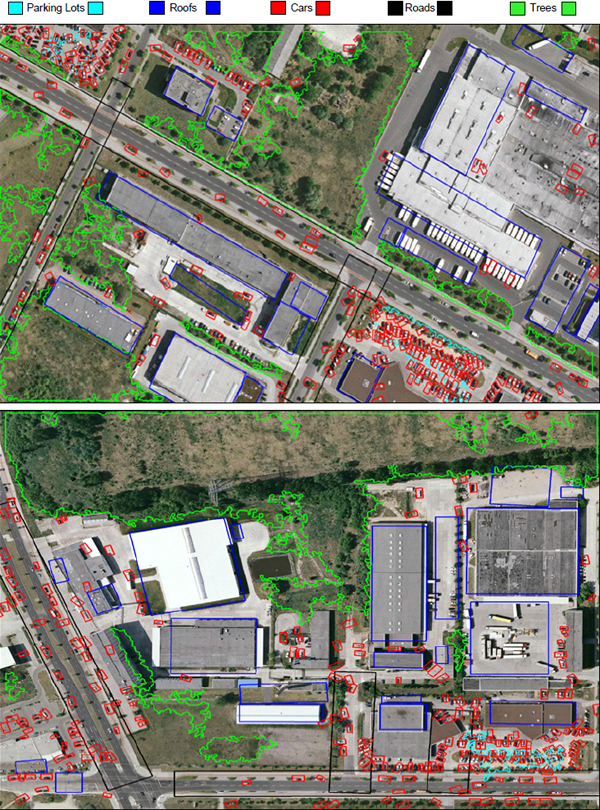
figure 8: flat configurations of parsed images.

References